九大排序算法的实现方法及算法分析
排序(Sorting)是计算机程序设计中的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个关键字有序的序列。
排序算法就是如何使得记录按照要求排列的方法,排序算法在很多领域得到相当地重视,尤其是在大量数据的处理方面,今天,马海祥就为大家简要介绍一下常用的九大排序算法,及利用JavaScript代码的实现方法及算法分析。
一、插入排序
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法,据马海祥了解它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
1、算法描述和实现
一般来说,插入排序都采用in-place在数组上实现,具体算法描述如下:
(1)、从第一个元素开始,该元素可以认为已经被排序;
(2)、取出下一个元素,在已经排序的元素序列中从后向前扫描;
(3)、如果该元素(已排序)大于新元素,将该元素移到下一位置;
(3)、重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
(4)、将新元素插入到该位置后;
(5)、重复步骤2~5。
2、JavaScript代码实现:
function insertionSort(array) {
if (Object.prototype.toString.call(array).slice(8, -1) === 'Array') {
for (var i = 1; i < array.length; i++) {
var key = array[i];
var j = i - 1;
while (j >= 0 && array[j] > key) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = key;
}
return array;
} else {
return 'array is not an Array!';
}
}
3、算法分析
最佳情况:输入数组按升序排列 T(n) = O(n)
最坏情况:输入数组按降序排列 T(n) = O(n2)
平均情况:T(n) = O(n2)
二、二分插入排序
二分插入(Binary-insert-sort)排序是一种在直接插入排序算法上进行小改动的排序算法,其与直接插入排序算法最大的区别在于查找插入位置时使用的是二分查找的方式,在速度上有一定提升。
1、算法描述和实现
一般来说,插入排序都采用in-place在数组上实现,具体算法描述如下:
(1)、从第一个元素开始,该元素可以认为已经被排序;
(2)、取出下一个元素,在已经排序的元素序列中二分查找到第一个比它大的数的位置;
(3)、将新元素插入到该位置后;
(4)、重复上述两步。
2、JavaScript代码实现:
function binaryInsertionSort(array) {
if (Object.prototype.toString.call(array).slice(8, -1) === 'Array') {
for (var i = 1; i < array.length; i++) {
var key = array[i], left = 0, right = i - 1;
while (left <= right) {
var middle = parseInt((left + right) / 2);
if (key < array[middle]) {
right = middle - 1;
} else {
left = middle + 1;
}
}
for (var j = i - 1; j >= left; j--) {
array[j + 1] = array[j];
}
array[left] = key;
}
return array;
} else {
return 'array is not an Array!';
}
}
3、算法分析
最佳情况:T(n) = O(nlogn)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(n2)
三、选择排序
选择排序(Selection-sort)是一种简单直观的排序算法,它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾,以此类推,直到所有元素均排序完毕。
1、算法描述和实现
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果,具体算法描述如下:
(1)、初始状态:无序区为R[1..n],有序区为空;
(2)、第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中选出关键字最小的记录R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区。
(3)、n-1趟结束,数组有序化了。
2、JavaScript代码实现:
function selectionSort(array) {
if (Object.prototype.toString.call(array).slice(8, -1) === 'Array') {
var len = array.length, temp;
for (var i = 0; i < len - 1; i++) {
var min = array[i];
for (var j = i + 1; j < len; j++) {
if (array[j] < min) {
temp = min;
min = array[j];
array[j] = temp;
}
}
array[i] = min;
}
return array;
} else {
return 'array is not an Array!';
}
}
3、算法分析
最佳情况:T(n) = O(n2)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(n2)
四、冒泡排序
冒泡排序是一种简单的排序算法,它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来,走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
1、算法描述和实现
据马海祥博客收集的资料显示,其具体算法描述如下:
(1)、比较相邻的元素,如果第一个比第二个大,就交换它们两个;
(2)、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
(3)、针对所有的元素重复以上的步骤,除了最后一个;
(4)、重复步骤1~3,直到排序完成。
2、JavaScript代码实现:
function bubbleSort(array) {
if (Object.prototype.toString.call(array).slice(8, -1) === 'Array') {
var len = array.length, temp;
for (var i = 0; i < len - 1; i++) {
for (var j = len - 1; j >= i; j--) {
if (array[j] < array[j - 1]) {
temp = array[j];
array[j] = array[j - 1];
array[j - 1] = temp;
}
}
}
return array;
} else {
return 'array is not an Array!';
}
}
3、算法分析
最佳情况:T(n) = O(n)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(n2)
五、快速排序
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
1、算法描述和实现
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists),具体算法描述如下:
(1)、从数列中挑出一个元素,称为 "基准"(pivot);
(2)、重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边),在这个分区退出之后,该基准就处于数列的中间位置,这个称为分区(partition)操作。
(3)、递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
2、JavaScript代码实现:
方法一:
function quickSort(array, left, right) {
if (Object.prototype.toString.call(array).slice(8, -1) === 'Array' && typeof left === 'number' && typeof right === 'number') {
if (left < right) {
var x = array[right], i = left - 1, temp;
for (var j = left; j <= right; j++) {
if (array[j] <= x) {
i++;
temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
quickSort(array, left, i - 1);
quickSort(array, i + 1, right);
};
} else {
return 'array is not an Array or left or right is not a number!';
}
}
var aaa = [3, 5, 2, 9, 1];
quickSort(aaa, 0, aaa.length - 1);
console.log(aaa);
方法二:
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};
3、算法分析
最佳情况:T(n) = O(nlogn)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(nlogn)
六、堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法,堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
1、算法描述和实现
据马海祥博客收集的资料显示,其具体算法描述如下:
(1)、将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆,此堆为初始的无序区;
(2)、将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
(3)、由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn),不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
2、JavaScript代码实现:
/*方法说明:堆排序
@param array 待排序数组*/
function heapSort(array) {
if (Object.prototype.toString.call(array).slice(8, -1) === 'Array') {
//建堆
var heapSize = array.length, temp;
for (var i = Math.floor(heapSize / 2); i >= 0; i--) {
heapify(array, i, heapSize);
}
//堆排序
for (var j = heapSize - 1; j >= 1; j--) {
temp = array[0];
array[0] = array[j];
array[j] = temp;
heapify(array, 0, --heapSize);
}
} else {
return 'array is not an Array!';
}
}
/*方法说明:维护堆的性质
@param arr 数组
@param x 数组下标
@param len 堆大小*/
function heapify(arr, x, len) {
if (Object.prototype.toString.call(arr).slice(8, -1) === 'Array' && typeof x === 'number') {
var l = 2 * x, r = 2 * x + 1, largest = x, temp;
if (l < len && arr[l] > arr[largest]) {
largest = l;
}
if (r < len && arr[r] > arr[largest]) {
largest = r;
}
if (largest != x) {
temp = arr[x];
arr[x] = arr[largest];
arr[largest] = temp;
heapify(arr, largest, len);
}
} else {
return 'arr is not an Array or x is not a number!';
}
}
3、算法分析
最佳情况:T(n) = O(nlogn)
最差情况:T(n) = O(nlogn)
平均情况:T(n) = O(nlogn)
七、归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,归并排序是一种稳定的排序方法,将已有序的子序列合并,得到完全有序的序列,即先使每个子序列有序,再使子序列段间有序,若将两个有序表合并成一个有序表,称为2-路归并。
1、算法描述和实现
具体算法描述如下:
(1)、把长度为n的输入序列分成两个长度为n/2的子序列;
(2)、对这两个子序列分别采用归并排序;
(3)、将两个排序好的子序列合并成一个最终的排序序列。
2、JavaScript代码实现:
function mergeSort(array, p, r) {
if (p < r) {
var q = Math.floor((p + r) / 2);
mergeSort(array, p, q);
mergeSort(array, q + 1, r);
merge(array, p, q, r);
}
}
function merge(array, p, q, r) {
var n1 = q - p + 1, n2 = r - q, left = [], right = [], m = n = 0;
for (var i = 0; i < n1; i++) {
left[i] = array[p + i];
}
for (var j = 0; j < n2; j++) {
right[j] = array[q + 1 + j];
}
left[n1] = right[n2] = Number.MAX_VALUE;
for (var k = p; k <= r; k++) {
if (left[m] <= right[n]) {
array[k] = left[m];
m++;
} else {
array[k] = right[n];
n++;
}
}
}
3、算法分析
最佳情况:T(n) = O(n)
最差情况:T(n) = O(nlogn)
平均情况:T(n) = O(nlogn)
八、桶排序
桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。
1、算法描述和实现
具体算法描述如下:
(1)、设置一个定量的数组当作空桶;
(2)、遍历输入数据,并且把数据一个一个放到对应的桶里去;
(3)、对每个不是空的桶进行排序;
(4)、从不是空的桶里把排好序的数据拼接起来。
2、JavaScript代码实现:
/*方法说明:桶排序
@param array 数组
@param num 桶的数量*/
function bucketSort(array, num) {
if (array.length <= 1) {
return array;
}
var len = array.length, buckets = [], result = [], min = max = array[0], regex = '/^[1-9]+[0-9]*$/', space, n = 0;
num = num || ((num > 1 && regex.test(num)) ? num : 10);
for (var i = 1; i < len; i++) {
min = min <= array[i] ? min : array[i];
max = max >= array[i] ? max : array[i];
}
space = (max - min + 1) / num;
for (var j = 0; j < len; j++) {
var index = Math.floor((array[j] - min) / space);
if (buckets[index]) { // 非空桶,插入排序
var k = buckets[index].length - 1;
while (k >= 0 && buckets[index][k] > array[j]) {
buckets[index][k + 1] = buckets[index][k];
k--;
}
buckets[index][k + 1] = array[j];
} else { //空桶,初始化
buckets[index] = [];
buckets[index].push(array[j]);
}
}
while (n < num) {
result = result.concat(buckets[n]);
n++;
}
return result;
}
3、算法分析
桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n),很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少,但相应的空间消耗就会增大。
九、计数排序
计数排序(Counting sort)是一种稳定的排序算法,计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数,然后,根据数组C来将A中的元素排到正确的位置,它只能对整数进行排序。
1、算法描述和实现
具体算法描述如下:
(1)、找出待排序的数组中最大和最小的元素;
(2)、统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
(3)、对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
(4)、反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
2、JavaScript代码实现:
function countingSort(array) {
var len = array.length, B = [], C = [], min = max = array[0];
for (var i = 0; i < len; i++) {
min = min <= array[i] ? min : array[i];
max = max >= array[i] ? max : array[i];
C[array[i]] = C[array[i]] ? C[array[i]] + 1 : 1;
}
for (var j = min; j < max; j++) {
C[j + 1] = (C[j + 1] || 0) + (C[j] || 0);
}
for (var k = len - 1; k >=0; k--) {
B[C[array[k]] - 1] = array[k];
C[array[k]]--;
}
return B;
}
3、算法分析
当输入的元素是n个0到k之间的整数时,它的运行时间是O(n+k),计数排序不是比较排序,排序的速度快于任何比较排序算法。
由于用来计数的数组C的长度取决于待排序数组中数据的范围(等于待排序数组的最大值与最小值的差加上1),这使得计数排序对于数据范围很大的数组,需要大量时间和内存。
马海祥博客点评:
一个优秀的算法可以节省大量的资源,在各个领域中考虑到数据的各种限制和规范,但要得到一个符合实际的优秀算法,就得经过大量的推理和分析。
本文发布于马海祥博客文章,如想转载,请注明原文网址摘自于https://www.mahaixiang.cn/seoyjy/877.html,注明出处;否则,禁止转载;谢谢配合!上一篇:301永久重定向的设置方法大全
下一篇:黑帽客如何利用黑帽SEO做快速排名谋取暴利
您可能还会对以下这些文章感兴趣!
-

落地页体验白皮书5.0解读:如何合理设置展开全文功能
本文解读文章深度剖析展开全文功能的设置要求。白皮书5.0提到”展开全文的设置必须具有文字标示,且功能实际可用;展开全文功能最多只能出现一次,但不可出现在落地页的首屏内容中(列表页除外);展开全文与广告等引导性内容要设置一定距离间隔,避免干扰用户操作。”如何设置展开全文按钮才更符合用户的体验习惯呢?这篇文章将为你答疑解惑。百度搜索用户研究团队的用户调研发现,搜索用户进入落地页的诉求是浏览页面全部内容,展开……【查看全文】
-

404 Not Found错误页面的解决方法和注意事项
404页面就是当用户访问某网站时,点击了错误的链接时,所返回的页面。最常见的出错提示:404 Not Found。其目的就是告诉浏览者其所请求的页面不存在或链接错误,同时引导用户使用网站其他页面而不是关闭窗口离开。错误页面的文字可以自定义,有些网站没有设置404错误页面,或……【查看全文】
-

网站SEO优化的分析诊断报告包含了哪些内容
SEO优化是针对搜索引擎规则做出优化以提高网站排名为目的的优化手段。其所需时间往往是长久性的,包括从网站域名、服务器、程序选取、网站结构、行业分析、竞争分析而切入的优化过程。而SEO诊断,在时间的要求上恰与其截然相反,所求目的完全与优化过程一致:提高网站友……【查看全文】
-

落地页体验白皮书5.0解读:什么样的顶部嵌入广告符合体验标准
《百度APP移动搜索落地页体验白皮书5.0》对页面广告的内容、形式、位置和面积的要求都做出了详细的说明,受到了全网开发者的广泛关注。关于白皮书5.0中最新提出的顶部嵌入广告标准”落地页首屏顶部允许嵌入不超过一屏面积10%的优质广告”,不少开发者对此提出疑问和反馈,本篇文章将对顶部嵌入优质广告要求做出具体解读:落地页首屏顶部允许嵌入优质广告的总体要求如下:面积:顶部嵌入广告面积必须小于首屏面积的10%。标识:广告位上有明……【查看全文】
-

百度索引量下降的原因及解决方法
作为一名专业的SEO人员,我们很多的时候都在研究站点中有多少页面可以作为搜索候选结果,也就是一个网站的索引量,所谓网站索引量,就是搜索引擎抓取你网站的数量,这能影响到网站收录率,是一个非常重要的SEO因素,索引量是流量的基础,索引量数据的每一个变动都拨动着……【查看全文】
-

揭秘搜索引擎中的反SEO作弊研究
从搜索引擎优化服务开始,分析了现在所存在的搜索引擎优化的作弊手段;然后提出了四种方法用来预防、破解作弊,并结合现实总结提出逐级分层审查刮度;最后结合Google搜索引擎,讨论并分析了Google搜索引擎的反作弊方法及其中的PR值算法……【查看全文】
-

《百度搜索优质内容指南》全文解读
今日,《百度搜索优质内容指南》在百度搜索学院悄悄地上线了,这是百度近两年,再次重新深度定义什么是百度搜索优质内容,对于SEO人员而言,特别是对于新站长而言,具有非常积极的指导意义,以免造成过多的资源浪费,给予了明确的指导规范的建议。百度搜索2020年全新发布了面向全网内容生产者的《百度搜索优质内容指南》,详细讲述了优质内容的标准,希望给广大内容生产者在生产优质内容时提供参考。关于优质内容的详细标准,请查看以下……【查看全文】
-

反向链接是什么意思
反向链接又叫导入链接(Backlinks),外部链接,是指外部网站有你的网址指向你的网站,其实就是在目标文档(网页)内部进行声明,要求目标文档指向自己(网页)的链接,通俗点讲,网页A上有一个链接指向网页B,则网页A上的链接是网页B的反向链接,换言之,常规链接在文……【查看全文】
阅读:2048关键词: 反向链接 日期:2012-08-14 -

Google搜索质量小组专业解答的25个SEO问题
2013年对于众多站长和SEO可以说是最为波折的一年,这一年百度出台了百度绿萝算法、百度石榴算法和百度绿萝算法2.0,而google也相继出台了谷歌EMD算法、熊猫算法、企鹅算法2.0和蜂鸟算法。作为一个站长或SEOer,你是否对这些算法还存在很多的疑惑,尤其对于靠做外贸产品……【查看全文】
-

linux系统或windows+iis系统设置404页面方法
404页面通常是为用户访问了网站上不存在或已删除的页面,服务器返回404错误页面,告诉浏览者其所请求的页面不存在或链接错误,同时引导用户使用网站其他页面而不是关闭窗口离开,消除用户的疑虑。网站设置404页面后,如果网站出现死链接,搜索引擎蜘蛛爬行这类网址……【查看全文】
-

百度移动搜索落地页体验白皮书4.0全文解读
进入移动互联网时代,百度搜索致力于提升搜索用户的浏览体验,营造健康的搜索生态。过去一年中,在百度搜索和全网资源提供者的共同努力下,移动搜索落地页广告问题已经得到了明显的改善。现在,百度搜索发布《百度移动搜索落地页体验白皮书4.0》,旨在继续与各内容生产……【查看全文】
-

百度排名算法规则及SEO优化要点总结
做SEO目的其实就是为访客服务,满足用户的需求,想方设法的为了用户提供他们想要看的内容,而不是一味的最求最大利益化,其实百度只是一个展示的平台,只要你有了用户的青睐,你想达到的目标,自然也就水到渠成了,做SEO的核心就是要挖掘用户的力量,只有挖掘用户的力量……【查看全文】
-

网站最新SEO优化公式解析
网站seo优化公式 SEO=Clock=C1+L2+K3+O4 1、是一个积分符号,C=content,L=link,K=keywords,O=others。SEO就是一个长期的对时间积分过程,内容是核心; 2、C1丰富的内容是第一位的要素,按照原创、伪原创、转载依次排列内容的重要性满足用户体验; 3、L2链接的合理与……【查看全文】
-

SEO链轮是什么?
SEO链轮(SEO Link Wheels)是从国外引入国内的,一种比较新颖的SEO策略,是一种比较先进的网络营销方式。SEO链轮是指通过在互联网上建立大量的独立站点或是在各大门户网站上开设博客,这些独立站点或是博客群通过单向的、有策略、有计划紧密的链接,并都指向要优化的目标……【查看全文】
-
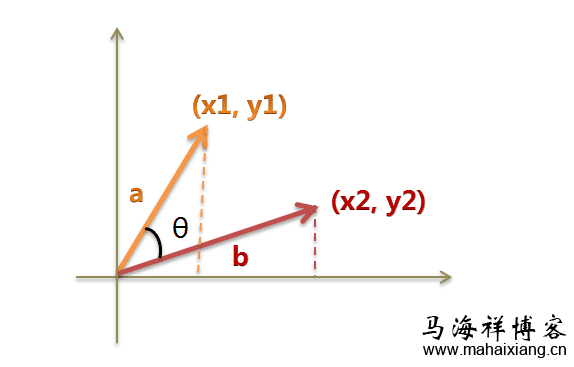
搜索引擎判定相似文章网页的原理
余弦相似性是指通过测量两个向量内积空间的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1,而其他任何角度的余弦值都不大于1;并且其最小值是 -1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时,余弦相似度的值……【查看全文】
-

基于用户投票的六大排名算法研究
随着互联网的发展,网站的数量也在随着成倍的增加着,就中国的互联网来说,根据中国互联网信息中心的数据显示,目前中国的网站数量每半年都会以接近10%的数量增长。这些大量的网站涌现,也就意味着我们已进入了信息大爆炸的时代。 而如今用户担心的已不再是信息太少,而……【查看全文】
-

百度快照更新是什么意思?
最近发现有很多刚入SEO行业的新手对网站seo的技巧有很多的误区,比如网站快照不更新就代表网站被惩罚。关于这个观点我们先看看什么是百度快照,百度快照的作用是什么?我们有该如何让百度快照持续更新呢?快照即为Web Cache,可以翻译为网页缓存,当搜索引擎派出蜘蛛去对网站……【查看全文】
-

2011-2012年百度历次大更新数据分析
本篇文章记录了百度从2011年到2012年中旬百度大更新记录的文章。以下数据分析以站长之家官方提供的网站监控分析数据为蓝本,结合优词网等站点观察数据和一些 优秀SEO站长工具和软件的收集,并佐以自己手上二十几个站点作参考进行综合分析,基于统计学分析原理,以大量站……【查看全文】
-
百度最新调整后的算法规则
最近闹得沸沸扬扬的百度6.22和6.28的K站事件到目前已经告一段落了,K站的主要原因已经渐渐明朗,以及百度将会对哪些类型的网站会做降权处理,现在也已经明朗化。针对各大站长漫长的着急等待,以及愤恨的心情,百度目前已经给出了较为明确的答案,那么百度规则和算法调整……【查看全文】
-

如何分析网站是否真的被降权惩罚及解决方法
对于混迹于国内站长圈的朋友来说,每天起早贪黑发外链的网站被百度惩罚似乎在这几年已经是司空见惯的事了,所以很多时候网站流量、排名或者是收录有小幅度波动时,站长都会认为网站又被惩罚了,有到处的去抱怨。其实,很多情况都只是站长自己太过于敏感了而已,网站被百……【查看全文】
分类目录
互联网更多>>
 云服务器的常规安全设置及基本安全策略
我们要保障云服务器数据安全,首先应树立正确的安全意识,从监控、入侵防御、数据备份等多方面做好安全措施,……
云服务器的常规安全设置及基本安全策略
我们要保障云服务器数据安全,首先应树立正确的安全意识,从监控、入侵防御、数据备份等多方面做好安全措施,……
 基于贝叶斯推断应用原理的过滤垃圾邮件研究
随着电子邮件的应用与普及,垃圾邮件的泛滥也越来越多地受到人们的关注。而目前正确识别垃圾邮件的技术难度非……
基于贝叶斯推断应用原理的过滤垃圾邮件研究
随着电子邮件的应用与普及,垃圾邮件的泛滥也越来越多地受到人们的关注。而目前正确识别垃圾邮件的技术难度非……
 互联网技术的50年发展回顾与分析
1998年至2008年是公认的互联网飞速发展的十年,无论是传输速率、网络规模、关键技术还是应用领域都经历了大幅的增……
互联网技术的50年发展回顾与分析
1998年至2008年是公认的互联网飞速发展的十年,无论是传输速率、网络规模、关键技术还是应用领域都经历了大幅的增……
SEO优化 更多>>
-
 医疗行业该如何做免费营销推广
医疗行业该如何做免费营销推广
当前医疗网站越来越多,竞争也越来越激烈,各…… -
 医疗行业开展品牌推广急需解决的1
医疗行业开展品牌推广急需解决的1
如今医疗行业要想在互联网上占有一席之地,就…… -
 百度公告:关于近期出现网站劫持用
百度公告:关于近期出现网站劫持用
近日,百度搜索技术团队发现,搜索结果中的部…… -
 移动设备前端开发中viewport的理论及使
移动设备前端开发中viewport的理论及使
在移动设备上进行网页的重构或开发,首先得搞…… -
 百度对站点Logo属性审核原则的具体要
百度对站点Logo属性审核原则的具体要
自百度搜索资源平台后台的站点属性设置开通上…… -
 未来的站内SEO优化需要做些什么?
未来的站内SEO优化需要做些什么?
SEO说难不难,说简单也不是那么简单,很多人问…… -
 预约未到诊患者的回访技巧及话术整
预约未到诊患者的回访技巧及话术整
很多朋友问预约是否有技巧,个人认为技巧是沉…… -
 外贸企业网站常用的5个优化推广方法
外贸企业网站常用的5个优化推广方法
做海外推广不同国内的网站推广,因为在文化、……


 在服务器上设置网站IIS日志的方法步骤
在服务器上设置网站IIS日志的方法步骤 百度中文分词技术是什么?
百度中文分词技术是什么? 什么是白帽seo?
什么是白帽seo? 运营数据中常见的数据陷阱
运营数据中常见的数据陷阱 移动设备Web App开发与调试的相关知识要点
移动设备Web App开发与调试的相关知识要点 如何撰写一份产品体验报告?
如何撰写一份产品体验报告? 产品经理该如何做好产品的架构和流程
产品经理该如何做好产品的架构和流程 APP消息推送的误区与真相
APP消息推送的误区与真相 传统行业该如何做电子商务?
传统行业该如何做电子商务? O2O营销模式的深入解析
O2O营销模式的深入解析 中小站长常用的5种赚钱方法
中小站长常用的5种赚钱方法 生活中的一些好点子教会你如何赚钱
生活中的一些好点子教会你如何赚钱 知乎问答社区的运营机制
知乎问答社区的运营机制



 织梦dedecms列表页实现无限下拉加载效果的方法技巧
织梦dedecms列表页实现无限下拉加载效果的方法技巧  网站CSS代码优化的7个原则
网站CSS代码优化的7个原则  交互设计的三要素:目标、任务和行为
交互设计的三要素:目标、任务和行为 
